Логолинейная диагональ в волновом анализе

Главная страница Теория волн Эллиотта Логолинейная диагональ в волновом анализе

В марте 2025 года в Telegram-чате TRADE WAVES модель, обладающая дуальностью формы в зависимости от выбранного масштаба (линейного или логарифмического), получила ёмкое название «Логолинейная диагональ». Во вступительной части нашего материала предлагаю ознакомиться с кратким определением, изложенным в глоссарии:

Логолинейная диагональ (вариант перевода — Log-Linear Diagonal) — это разновидность модели волн Эллиотта, которая может быть воспринята одновременно двумя способами: как «сужающаяся» и как «расширяющаяся» диагональ. Преобразование формы происходит при переходе между линейным и логарифмическим масштабами.

Правила построения модели (в части соотношений подразделений) при измерении в логарифмическом масштабе следует интерпретировать в процентах, тогда как в линейном масштабе, напротив, — в абсолютных величинах, то есть в пунктах.

Данная разновидность диагонали заслуживает отдельного места в классификации моделей волн Эллиотта и в ближайшее время будет внесена в наше декомпозитное дерево.

Масштаб — какой выбрать

Давно прошли времена, когда ценовые графики строили с помощью карандаша и линейки на полулогарифмической бумаге. Сегодня, в эпоху компьютерных технологий, вы без труда построите любой график — перестроите с линейного на логарифмический.

И тут встаёт вполне закономерный вопрос: в каком масштабе следует проводить измерения? На какой шкале должны быть соблюдены правила построения волн Эллиотта.

Исходя из своего опыта в подсчёте, могу сказать следующее:

В обоих случаях — и на линейном, и на логарифмическом графиках — необходимо соблюдать соотношения между субволнами согласно установленным правилам. При этом форма модели может меняться в зависимости от выбранного масштаба. Например, в линейном масштабе модель имеет форму сужающейся диагонали, а в логарифмическом — расширяющейся.

Это, на мой взгляд, ценное наблюдение я включил в свод правил и норм.

Как же так происходит, что модель меняет форму при переходе между линейным и логарифмическим масштабами?

Один из моих некогда хороших товарищей Александр описал это явление так:

Если разница цены начала диагонали и её окончания в процентах невелика, то диагонали будут выглядеть одинаково. Однако если эти цены отличаются в разы, то в логарифмическом масштабе длина каждого доллара первой волны восходящей диагонали будет содержать больше пикселей на ценовой оси, чем тот же доллар в волне пятой. То есть первые волны на графике растягиваются, а последние сужаются. Таким образом, расширяющаяся в линейном масштабе диагональ лёгким движением логарифмической шкалы превращается в сужающуюся диагональ.

Подобную картину вы часто будете встречать на сильно растущих или резко падающих рынках — на графиках с большим разбросом цен.

Теперь давайте разберём пару наглядных примеров, посмотрим, как полученные знания могут помочь в проверке на валидность развёрнутых фигур, а также в определении критических уровней и минимальных целей для развивающихся моделей.

Условимся, что нам заранее достоверно известно: подъём или снижение идёт в рамках третьей волны диагонали. Допустим, первая волна в развивающейся модели является множественным зигзагом без возможности дальнейшего усложнения.

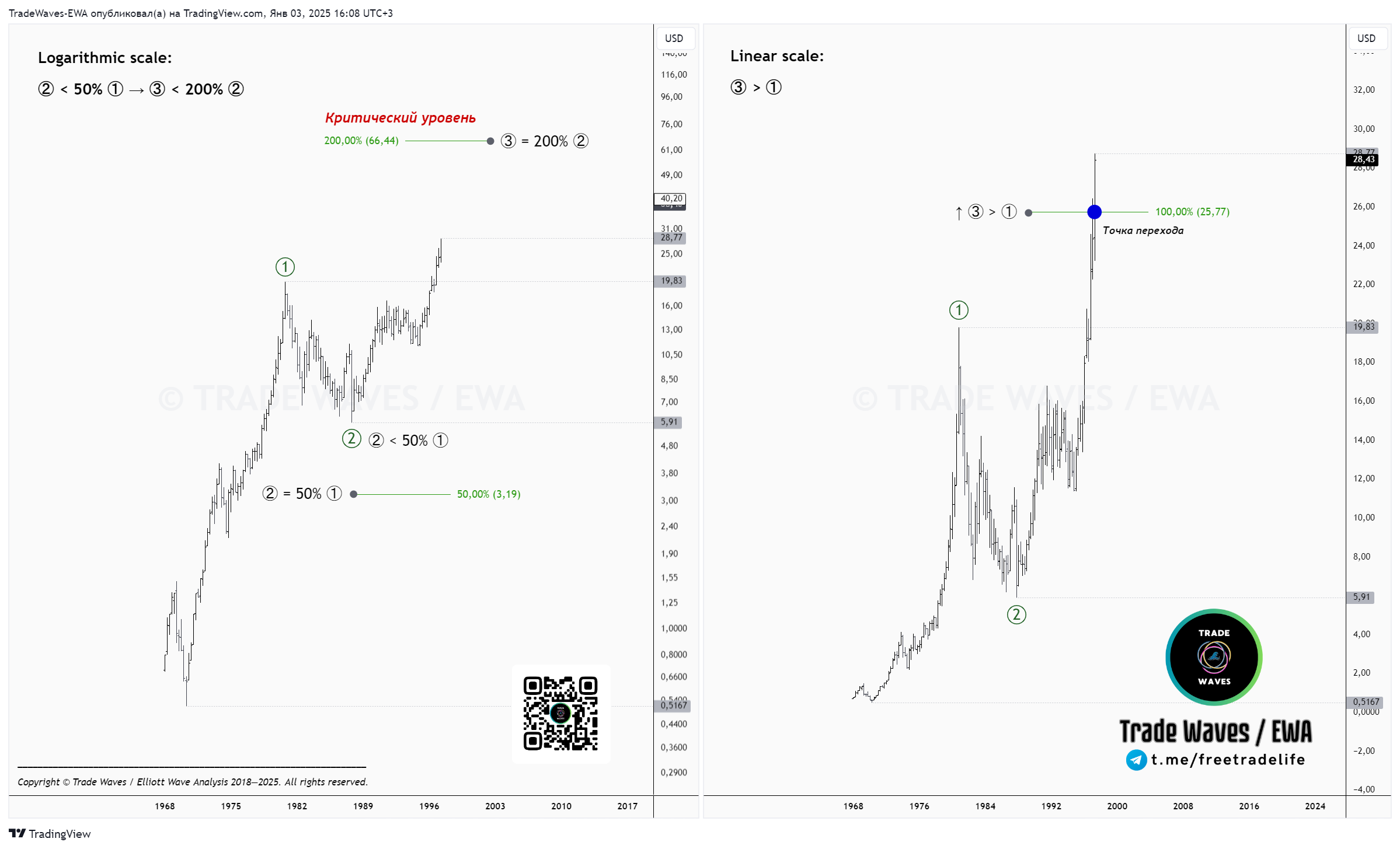
Отслеживая длину третьей волны одновременно на двух шкалах — логарифмической (рис. 1 — слева) и линейной (рис. 2 — справа), можно столкнуться с ситуацией, когда на одной из шкал нарушается правило «③ < ①», регулирующее построение сужающейся диагонали. Давайте назовём этот момент точкой перехода.

Исходя из своего опыта в подсчёте, могу сказать следующее:

Это, на мой взгляд, ценное наблюдение я включил в свод правил и норм.

Как же так происходит, что модель меняет форму при переходе между линейным и логарифмическим масштабами?

Один из моих некогда хороших товарищей Александр описал это явление так:

«Если разница цены начала диагонали и её окончания в процентах невелика, то диагонали будут выглядеть одинаково. Однако если эти цены отличаются в разы, то в логарифмическом масштабе длина каждого доллара первой волны восходящей диагонали будет содержать больше пикселей на ценовой оси, чем тот же доллар в волне пятой. То есть первые волны на графике растягиваются, а последние сужаются. Таким образом, расширяющаяся в линейном масштабе диагональ лёгким движением логарифмической шкалы превращается в сужающуюся диагональ.»

Отслеживая длину третьей волны одновременно на двух шкалах — логарифмической (рис. 1 — слева) и линейной (рис. 1 — справа), можно столкнуться с ситуацией, когда на одной из шкал нарушается правило «③ < ①», регулирующее построение сужающейся диагонали. Давайте назовём этот момент точкой перехода.

Масштаб и форма

Итак, какие заключения мы можем сделать, исходя из реальной рыночной ситуации, приведённой на рис. 1:

Дальнейшее построение диагонали в линейном масштабе возможно только по пути развития расширяющейся формы модели, внутри которой ③ > ①, ④ > ② и ⑤ > ③.
В логарифмическом масштабе сужающаяся диагональ остаётся валидной, критическим уровнем выступает отметка ③ = 200% ② (почему так — смотрели тут).

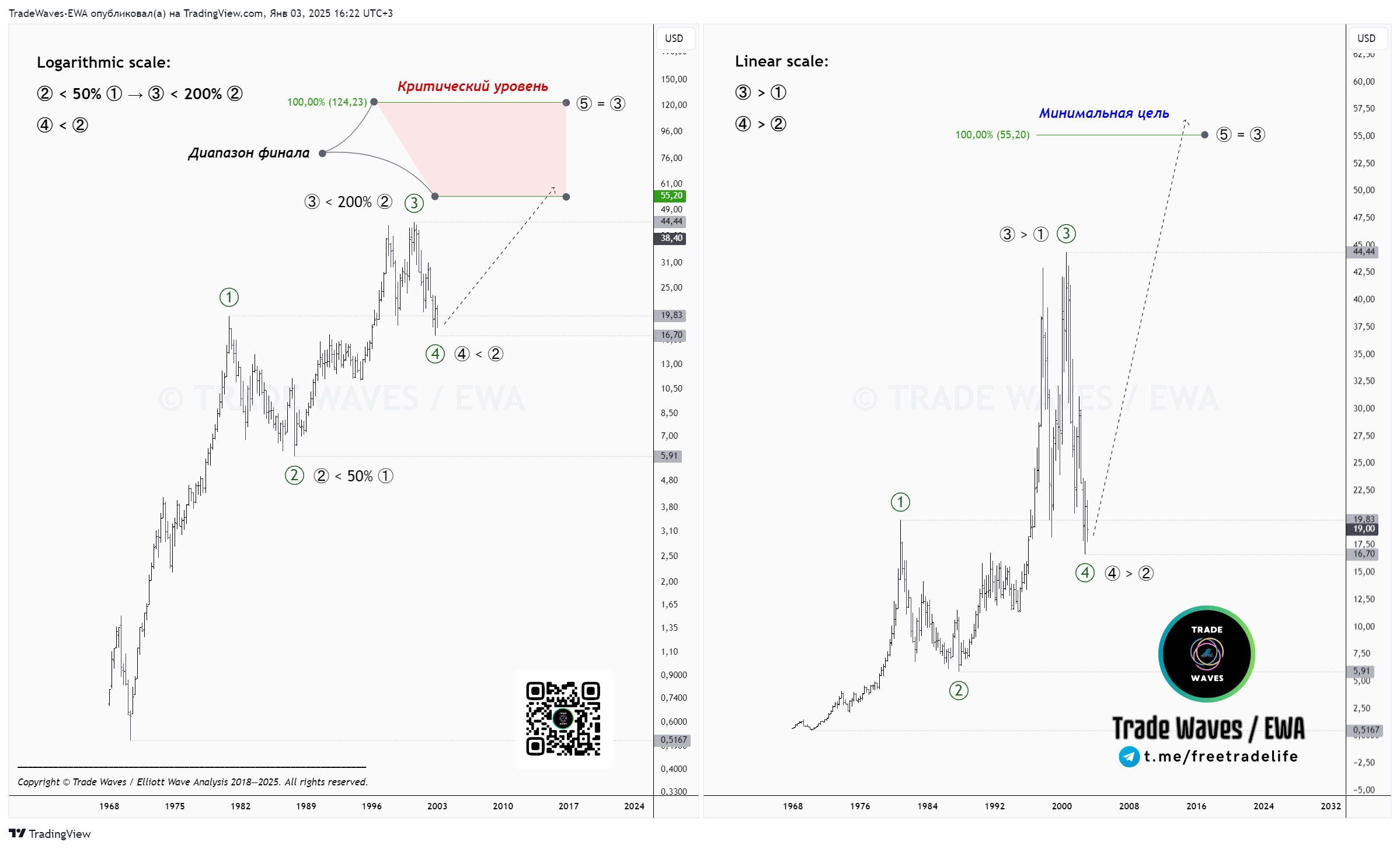
Касаясь второго пункта, важно отметить, что если будет пробит данный уровень, то и в логарифмическом масштабе следует отслеживать расширяющуюся форму модели. Назовём это точкой перехода 2.

Спустя время мы наблюдаем картину, когда минимальные требования волнами ③ и ④ исполнены как для сужающейся, так и расширяющейся диагонали, в зависимости от масштаба, на котором проводятся измерения. Так, на лог. шкале волна ③ не более 200% ②, а следующая за ней ④ перекрыла ①, сохранив правило ④ < ②. На линейной шкале правила выполняются для расширяющегося типа диагонали: волна ③ > ①, ④ > ②.

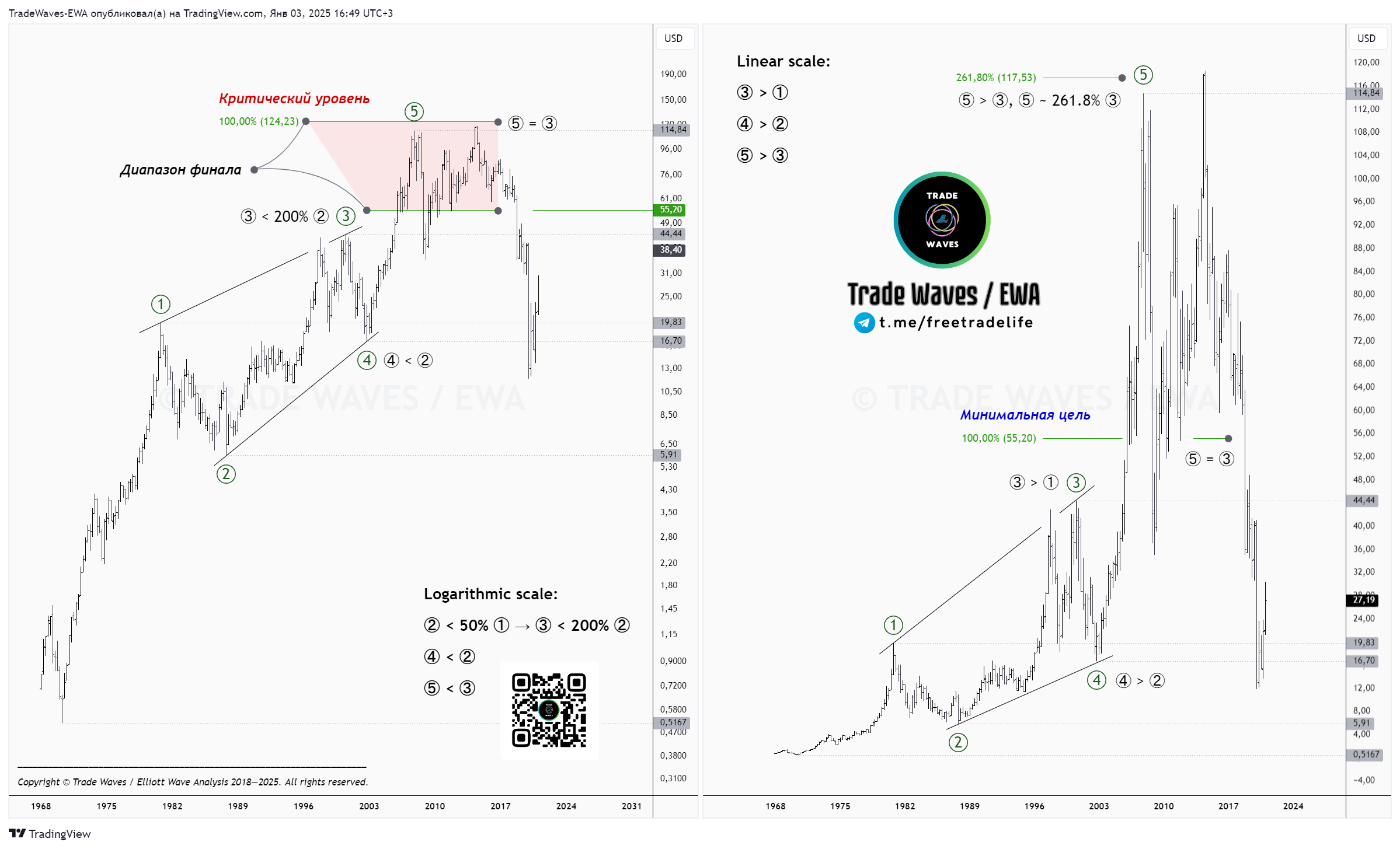
Далее мы можем определить диапазон финала для заключительной ⑤: ценовая область, включающая минимальную цель, при измерении на линейной шкале, то есть ⑤ > ③, и критический уровень, что будет построен на лог. шкале, а это — ⑤ = ③.

Как видим, в конкретном примере рынок развернул клиновидную структуру, которая может быть идентифицирована в качестве диагонали на обеих шкалах. Яркий пример валидной фигуры. Но так происходит не всегда. В ряде случаев при измерении абсолютных и относительных соотношений между подразделениями, которые отражает логарифмическое и линейное масштабирование соответственно, мы будем сталкиваться с нарушением правил. Например, длина волны ④ согласуется с сужающейся диагональю на лог. шкале, но не исполняет минимальных требований при рассмотрении в линейном масштабе, где ожидается диагональ другой формы. Последнее будет считаться нарушением правил и потребует пересмотра вашего каунта.

Данная техника построения целей и проверки валидности фигур имеет крайне высокую прогностическую ценность: имея развивающуюся диагональ на стадии зарождения третьей волны, проецируя критические уровни и минимальные цели на обеих шкалах, вам открывается возможность построить диапазон финала ④ и заключительной пятой волны.

Вся информация, размещённая на сайте tradewaves.ru, публикуется исключительно в ознакомительных и консультационных целях и не является индивидуальной инвестиционной рекомендацией, либо предложением приобрести ценные бумаги или иные финансовые инструменты. Администрация сайта не несёт ответственности за возможные убытки, возникшие в результате использования предоставленной информации.